There are two basic configurations
of three-phase power, delta and wye. An understanding of these two
types of power may be important for the safe operation of
three-phase equipment.
Wye Three-Phase
Three-phase power is most commonly
provided by the electric utility in a wye configuration. The main
advantage to wye power is that the phase-to-neutral voltage is equal
on all three legs. This is an important consideration because
three-phase lines are the backbone of the electrical distribution
system, and three-phase service is commonly provided to large
buildings and facilities to power both three-phase loads and 120
volt single-phase loads. In North America electrical systems, 120
volt power is almost always derived from a phase to neutral
connection. This is true of both single-phase service, which is
provided as 120/240 volt, and three-phase service as 120/208Y.
In the above systems, 120 volts is
derived from a phase-to-neutral connection in both cases. The 240
volts of the single-phase system and the 208 volts of the
three-phase system are both derived as phase-to-phase voltages. In
order to have 120 volts from phase to neutral on both systems, the
phase-to-phase voltages of the systems must be different. This can
best be understood with the help of the phase vector diagrams in
figures 1 and 2.
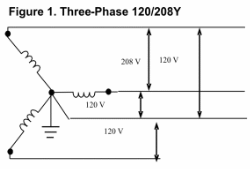
Figure 1 represents 120/208V wye,
which is delivered with four wires composed of one wire for each
voltage and a neutral. Each of the three voltages are 120 degrees
apart and have a common connection to ground and neutral (which are
at the same potential) represented by the dot in the middle. The
voltage measured between any two phases would be 208V, while any
phase-to-neutral voltage would be 120V. The relationship between
these voltages can be expressed mathematically. Specifically, in a
wye configured system, the phase-to-neutral voltage is equal to the
phase-to-phase voltage divided by the square root of three, or 208V
/ 1.73 = 120V. Thus, the phase-to-phase voltage must be 208V in
order to get 120V from the system.
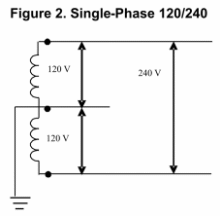
Figure 2 represents 120/240V
single-phase with two voltages 180 degrees apart with neutral and
ground halfway between the two voltages. The voltage measured
between the two legs is 240V, and since neutral is halfway between,
the voltage from either leg to neutral would be 120V.
In rare instances, three-phase
power from the electric utility is configured as 120/240V delta.
This is represented in Figure 3.
In this
configuration, ground and neutral are not referenced equally to the
three legs, but are half-way between the voltage derived from two of
the legs. As you can see, the voltage from leg 1 or leg 2 to
neutral would be 120V, but the voltage from the third leg will
|
be much higher,
approximately 208 volts. With 120/240V delta three-phase,
single-phase 120V equipment must never be powered by deriving a
phase-to-neutral voltage from the third phase because it will be 208
volts. Because of this high voltage to ground and neutral, this leg
is often referred to as the “high leg”.
Delta Configured Three-Phase Power from a Phase
Converter
Nearly all phase converters produce
three-phase power by generating a voltage that is added to the two
legs of single-phase. The phase vector diagram in Figure 3 helps to
illustrate how this is accomplished.
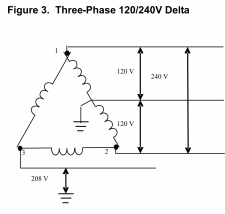
In the figure, 1 and 2 represent the two
legs of single-phase service which are 180 degrees apart and have a
potential of 240 volts between them. Ground and neutral
are halfway between these two voltages. The phase converter
generates voltage 3 at right angles to the voltage between 1 and 2.
If this voltage is generated at the proper level and at the correct
angle, it will create a triangle when referenced to voltages 1 and 2
of the single-phase service. In essence, it is the same as the
120/240V delta power sometimes provided by the utility that was
discussed earlier. The same warnings apply to deriving a
phase-to-neutral voltage from the third phase. While the
phase-to-neutral voltage from leg 1 or 2 is 120 volts, leg 3 to
neutral (and ground which is at the same potential as neutral) will
be approximately 208 volts. This is because in order to have
balance phase-to-phase voltages, voltage 3 must be equal to one-half
the voltage of leg 1 to leg 2 times the square root of three or,
240V / 2 = 120V x 1.73 = 208V.
If a piece of three-phase equipment
operates only on phase-to-phase voltages, it does not matter whether
the power is configured as wye or as delta. If none of the circuits
in the machine or the motor being operated derive a voltage by
referencing neutral/ground, the machine does not know or care where
ground/neutral is in reference to any of the phases. It only “sees”
the relationship between the phases. It is evident that if you
reference the three voltages of wye power and “erase” the connection
to ground/neutral, you have a triangle, the same as in delta
configured power. Only when equipment has single-phase 120V
circuits that are derived from phase-to-neutral connections does it
matter if the power is configured as wye or delta.
If the three-phase equipment has
120V phase-to-neutral circuits that cannot be isolated and connected
to either leg 1 or leg 2, the output of the phase converter must be
passed through a 240V delta to 120/208V wye isolation transformer.
This transformer will establish ground and neutral at equal distance
from all three legs and deliver the power in a wye configuration.
This is especially important when
operating some newer CNC machines that have certain Fanuc or Siemens
controls. These controls handle regenerative power from the spindle
motor by putting the regenerative power back onto the line utilizing
a phase-to-neutral connection on all three legs. If these machines
are powered by a phase converter with delta configured power, the
regen circuit on the leg manufactured by the phase converter will
operate at a voltage that is too high. An isolation transformer
must be used to convert the power from delta to wye configuration.
|
|